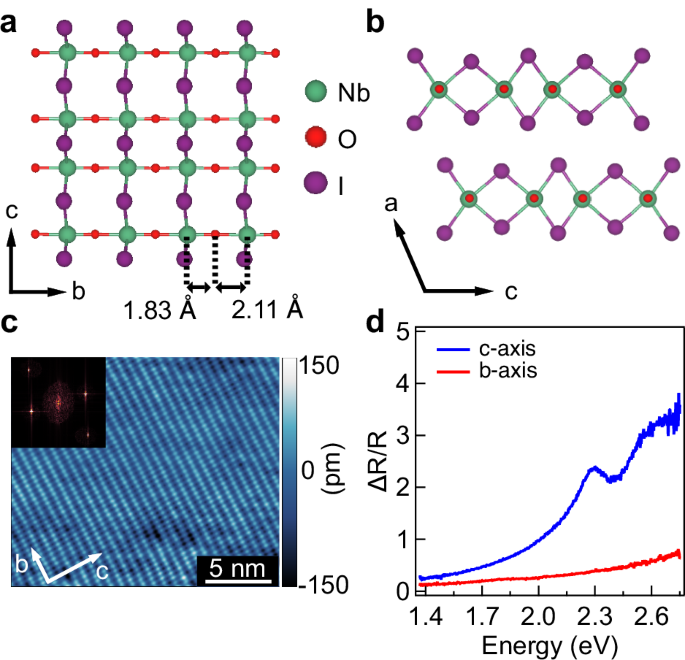
We grow millimeter-size single crystal NbOI2 with optically flat surfaces (Supplementary Fig. 1), using the chemical vapor transport method18 and confirm the phase purity through powder X-ray diffraction (Supplementary Fig. 1b). NbOI2 adopts a vdW layered monoclinic crystal structure in the C2 space group (Fig. 1a, b). Along the b-axis, the Nb atoms are displaced from the center position, resulting in unequal Nb−O bond lengths and spontaneous polarization along the b-axis. Scanning tunneling microscopy (STM) image (Fig. 1c) of the crystal surface freshly cleaved in vacuum confirms the rectangular in-plane structure with lattice parameters consistent with those obtained by single-crystal X-ray diffraction (Supplementary Fig. 2). The anisotropic in-plane crystal structure gives rise to an anisotropic electronic structure, as revealed by differential reflectance (ΔR/R) spectroscopy (Fig. 1d). The ΔR/R spectrum along the c-axis reveals above-gap transitions at 2.3 eV and 2.6 eV18; these transitions are absent along the b-axis. A weak onset in absorption is visible at ~ 1.1 eV (Supplementary Fig. 3), likely due to an indirect optical transition. By performing high-temperature second harmonic generation (SHG) and Raman spectroscopy, we also find the ferroelectric phase remains robust up to 573 K (Supplementary Fig. 4).

a, b Crystal structure of NbOI2 viewed perpendicular to bc-plane (a) and along b-axis (b). c. Scanning tunneling microscopy image of cleaved NbOI2 single crystal at room temperature (RT). The inset shows the FT of the topography. d Differential reflectance spectra of 7-layers NbOI2 on z-cut quartz with incident light polarized along either crystallographic c- or b-axis at RT. ΔR is defined as Rsample – Rsubstrate in steady state and R in the dominator is Rsubstrate.
To determine the phonon modes in NbOI2, we performed polarization-angle resolved Raman spectroscopy with incident polarization in the bc (yz) plane and scattered polarization parallel (pp) or perpendicular (cp) to incident polarization. The polarization angle (θ°) is referenced to the crystallographic c-axis. Fig. 2a, b present pseudo-color plots of Raman spectra with pp and cp polarizations, respectively, along with polar plots of the Raman peak intensities for the strongest mode at 3.137 ± 0.002 THz (104.5 cm−1, labeled as P2 in main text) in Fig. 2c. This mode is highly anisotropic and preferentially allowed along the b-axis for pp (red). For cross-polarization (blue), the polar plot is symmetric along the diagonals between the b- and c-axes. We conduct Raman tensor analysis to assign symmetries to the Raman-active phonons (see Supplementary Notes and Supplementary Fig. 5 for details)24,25,26,27. We extract line-cuts of the spectra at θ = 0° (c-axis) and 90° (b-axis) to show the anisotropy of the Raman-active modes (Fig. 2d). A comparison of the experimental data with theoretical Raman spectra calculated from first-principles DFT in Fig. 2e shows good agreement across the measured range (see Methods and Supplementary Table 1 for full assignment of calculated Raman modes). In particular, an excellent agreement can be confirmed for the anisotropy of the main phonon mode (this mode is 2.83 THz in computation, corresponding to the P2 mode in experiments), as shown in Fig. 2f. The discrepancy in the position of the small shoulder peak—down-shifted in the experiment (the P1 mode) and up-shifted in simulation—may be attributed to anharmonicity. While anharmonicity is experimentally evidenced by the temperature dependence of its full-width-at-half-maximum (FWHM) and center-frequency shift, Supplementary Fig. 4c and d, respectively, it is very challenging to include anharmonicity in computation28. Such computational effort is beyond the scope of the current study and may be of interest for the future28. As detailed below, the main phonon mode, P2, corresponds to the ferroelectric TO phonon and strongly couples to photogenerated carriers.

a, b Polarization-angle resolved Raman spectra of NbOI2 at RT with incident polarization in the yz plane (y = b-axis, z = c-axis) and scattering polarization parallel (a) or perpendicular (b) to incident polarization. 0 degree is referenced to the crystallographic c-axis. The color bar represents the Raman scattering intensity (normalized to the highest intensity for clarity). pp represents parallel polarization and cp represents cross polarization. c Polar plot corresponding to spectral cut from (a) and (b) at 3.137 THz mode (P2 mode). Solid lines are fitting curves obtained by the global fit to both pp and cp data with Supplementary Equations 1 and 2 in Supplementary Text, respectively. d Parallel polarized Raman spectrum with incident polarization aligned to either the b or c-axis. e Simulated Raman spectra at 300 K with parallel polarization. f Simulated polar plot of the phonon mode at a calculated frequency of 2.830 THz. An empirical term, \(\cos {\varphi }_{{\rm{c}}-{\rm{b}}}\), that was deduced from the tensor fit of the experimental P2 mode data and describing the phase difference between two tensor elements was applied to the simulation to account for the finite absorption of incident light.
We carry out ultrafast pump-probe coherent phonon spectroscopy (CPS) to probe how the electronic transition couples to phonons in NbOI2. We use an excitation laser pulse (pulse width ~ 150 fs) centered at hν1 = 2.58 eV, which is resonant with the second above-gap transition, with light incidence normal to the surface and polarization parallel to the c-axis. Fig. 3a and b show the transient reflectivity spectrum (ΔR/R0, where R0 is reflectance without the pump and ΔR is the pump-induced change in reflectance), probed by a broadband pulse (hν2 ~ 1.46 − 2.50 eV) polarized parallel to the c- or b-axis, respectively. In transient reflectance probed along the optical-transition allowed direction (c-axis), there is a clear signature of exciton bleaching at ~ 2.20 − 2.35 eV, with periodic modulation of the signal arising from coherent phonon(s). The clear oscillatory signals at delay times > 30 ps without subtracting the electronic signal demonstrate the long coherence time at room temperature with a decay constant of ~ 30 ps (also see Supplementary Fig. 6 for short-time Fourier transform analysis and fitting of the dephasing time). The full kinetic trace of exciton bleaching (Supplementary Fig. 7) can be described by a long decay time constant of τd = 5.6 ± 1.2 ns. After the removal of the incoherent decay component, the Fourier transform (FT) of the residue coherent signals (Fig. 3c and d) gives a single frequency centered at 3.125 ± 0.001 THz with a FWHM of 0.038 ± 0.001 THz (Supplementary Fig. 6). This oscillatory frequency closely matches the frequency of the P2 phonon mode observed in polarization-angle resolved Raman spectra.

a, b Transient reflectivity spectra of NbOI2 measured at RT for probe polarization parallel to c- (a) or b-axis (b). The color bar indicates the magnitude of ΔR/R0. c FT of the oscillatory components extracted from (a, b) at off-resonant probe region (1.55 eV). d FT of the oscillator components extracted from (a, b) at resonant probe region (2.30 eV).
The polarization dependencies of the CPS spectra for resonant and off-resonant probes show key differences. When probed with photon energy below the excitonic transition (off-resonant, Fig. 3c), the phonon mode dependence is highly anisotropic. The FT amplitude of the 3.125 THz peak is prominent with probe polarization along the b-axis (Ib) and more than one order of magnitude lower with polarization along the c-axis (Ic). The ratio Ic/Ib ~ 0.1 from CPS data (Fig. 3c) is close to the ratio Ic/Ib = 0.16 obtained from Raman spectroscopy (Fig. 2c), consistent with the symmetry of the Raman tensor. Moreover, the FWHMs of the peaks measured by CPS (0.038 ± 0.001 THz),) and Raman spectroscopy (0.039 ± 0.002 THz) are essentially the same. We conclude that with a non-resonant, below-gap probe, the P2 phonon mode revealed in CPS is determined by the same Raman tensor29,30 as in conventional Raman spectroscopy.
By contrast, when we use a resonant probe (Fig. 3d), the CPS spectrum reveals the breaking of the selection rule dictated by the Raman tensor. The weak coherent phonon amplitude for probe polarization along the c-axis becomes dominant with the resonant probe. The FT amplitude ratio Ic/Ib for the P2 mode increases from ~ 0.1 with the off-resonant probe to 2.6 with the resonant probe. We attribute the emergence of the intense symmetry-forbidden P2 mode to the strong coupling between the P2 mode and the above-gap electronic transition. This coupling can result from the displacement along the P2 phonon coordinate in the potential energy surface corresponding to the optical transition due to the strong electron-phonon coupling associated with the conduction band. Since the above-gap electronic transition is related to carrier generation, this strong coupling suggests the polaronic feature of the photoexcited carriers31,32. As we show below, the P2 mode is identified as a TO phonon mode.
To reveal the nature of the P2 phonon mode, we performed terahertz time-domain spectroscopy (THz-TDS) measurements in transmission geometry on a free-standing NbOI2 crystal with thickness ~ 2.6 µm (Supplementary Fig. 8). Because the transverse nature of electromagnetic wave only allows excitation of TO phonon modes, THz-TDS directly probes TO phonons. Fig. 4a and b show the time-domain waveforms and their corresponding FT spectra along the b- (red) and c- (blue) crystallographic axes, respectively. A full spectrum of THz absorption in frequency domain is shown in Supplementary Fig. 9. The strong THz absorption peak is observed at 3.130 ± 0.008 THz (Fig. 4b), and this frequency is the same as that of the exclusive mode observed in CPS (reproduced in Fig. 4c), and the main phonon peak observed in Raman spectra (the P2 mode, reproduced in Fig. 4d). These experiments confirm the TO nature of the P2 phonon mode. Therefore, we establish that the P2 TO mode is the only phonon mode that couples to the electronic transition, whereas no contribution from LO phonons is found. The absence of the commonly observed electron-LO-phonon coupling points to the uniqueness of a ferroelectric semiconductor.

a, b Polarization-dependent THz absorption spectra of a 2.6 μm thick NbOI2 in (a) time domain and (b) frequency domain, respectively. The reference signal represents the THz signal without transmitting through the NbOI2 sample. The shoulder peak at 3.044 ± 0.023 THz does not match the shoulder peak found in the Raman spectrum with its Raman shift being 2.98 THz. We assign the 3.04 THz mode to a different TO phonon with a relatively low Raman cross-section which is nonetheless IR active. c FT spectra of the oscillatory component at exciton-resonant region obtained from CPS. d Co-polarized Raman spectra of NbOI2 with off-resonant pump. e Calculated phonon dispersion based on first-principles DFT calculation with selected q directions. Here, A denotes a vector perpendicular to the crystallographic bc-plane, whereas Y denotes a vector parallel to the crystallographic b-axis. Color contrast represents different levels of transverse or longitudinal character. An additional phonon dispersion considering the vdW correction was performed and shown in Supplementary Fig. 11, which shows negligible difference from the current result. Supplementary Files include NbOI2 primitive cells optimized by the functions with and without the vdW correction. f Atomic motions (represented as blue arrows) of the TO phonon mode at 2.830 THz (calculated frequency of the P2 mode) viewed perpendicular to crystallographic bc-plane (top view) and along the c-axis (side view). Note that for graphing clarity, the length of the eigenvectors shown as arrows here do not represent the relative amplitude. The ratio of the relative amplitude of the eigenvectors for Nb and O (lNb/lO) is ~ 3.9.
To support our interpretation of experimental results, we theoretically model the phonon dispersion using DFT (Fig. 4e) and reveal the atomic motions that underlie the TO phonon mode (Fig. 4f). By computing the inner product of eigenvectors and phonon momentum, we can estimate the TO and LO character of each phonon mode at different momentum vector q in the phonon dispersion. Here, we define an inner product value of 0 as a full TO character, while a value of unity is defined as a full LO character. Along the Γ−A direction (perpendicular to the bc plane and parallel to the q adopted in all the optical experiments), the 2.830 THz phonon mode (3.130 THz from THz-TDs) is essentially purely TO near the zone center Γ, corroborating our THz-TDS results that indicate strong TO character of the P2 phonon mode. The same mode (2.830 THz along Γ−A in DFT) becomes highly longitudinal along the Γ−Y direction (parallel to the b-axis), and shifts to 3.128 THz (Supplementary Fig. 10 shows a clear track of the P2 mode near the Γ point). The discontinuity of frequency around the zone center, with the LO mode shifting to a higher frequency, is a signature of a polar phonon33. The TO-LO splitting at the zone center is ~ 1.21 meV in our calculations, manifesting the polar nature of this phonon mode along the direction associated with ferroelectric order.
Figure 4f shows the eigenvectors of the TO phonon mode. From both top and side views, we identify Nb and O atoms oscillating in-phase with different amplitudes, resulting in stretching and contraction of adjacent Nb-O-Nb bonds along the crystallographic b-axis and modulation of the local polarization. The calculated atomic motions are reminiscent of soft modes associated with displacive-type ferroelectrics; these soft modes are typically anharmonic along the direction associated with ferroelectric order. Although our calculations are based on the harmonic approximation, we expect anharmonicity in the TO phonon potential well due to its ferroelectric character. The asymmetric potential well, as a result of this anharmonicity of the TO phonon will induce a nonvanishing change in the local polarization of the material when the phonon propagates. Such local polarization fluctuations can couple to the electronic transition and modulate the band energies near the lowest direct transition as manifested in our CPS results shown above.
To further support the distinct nature of the coupling of the P2 TO mode to the electronic transition, we performed resonant inelastic X-ray scattering (RIXS) measurements21,22,23 at the O-K edge (1 s → 2p transition), Fig. 5. RIXS process here first excites a core electron, leaving a hole in the core level. This empty core is immediately filled by a valence electron with the emission of an X-ray photon which inelastically scatters phonons in the system. As such, RIXS probes electron-phonon coupling associated with the valence band, and this coupling is expected to be distinctly different from that between electronic transition and the ferroelectric TO mode. Using linearly polarized incident photons parallel to the b-axis (π-polarization) and to the c-axis (σ-polarization), we find an anisotropic response in the X-ray Absorption Spectroscopy (XAS) pre-edge (Fig. 5b) and in the high energy loss region (> ~ 2 eV) of the RIXS spectra (Fig. 5a). This anisotropic behavior is consistent with the differential reflectance spectra in Fig. 1c, and we associate it with the anisotropic electronic structure of NbOI2. In particular, the anisotropic hybridization between O 2p and Nb 4 d orbitals34,35,36,37 is revealed by the strong anisotropic XAS feature around 530 ~ 535 eV38. In the low energy loss (< 50 meV) regime of the RIXS spectrum, several spectral components overlap in the vicinity of the elastic line and are visible with both σ and π polarization. When fitting the data (Fig. 5c), we observe a resolution-limited mode at 7 meV, together with its second-order harmonic at 14 meV, and its anti-Stokes counterpart at − 7 meV. The 7 meV mode matches a phonon observed with THz spectroscopy (Supplementary Fig. 9) at 1.78 THz. The intensity ratio between the 7 and 14 meV modes and the evolution of their intensity as a function of incident photon energy supports our assignment of the second peak as the higher harmonic35,37. The presence of higher-order phonon harmonics in the RIXS spectra signifies a non-negligible electron-phonon coupling between valence electrons and the 7 meV phonon mode34,35,36,37. While we cannot fully rule out a small contribution of the P2 phonon mode (~ 12.9 meV or 3.13 THz) in the RIXS response, the coupling of valence-band electron to phonon is dominated by the 7 meV phonon mode. Distinct from this valence-band electron-phonon coupling scenario, CPS results have revealed that the P2 phonon mode dominates coupling to the above-gap electronic transition. Overall, the absence of a RIXS feature at ~ 3.13 THz supports our interpretation of the CPS data that points to an additional coupling mechanism beyond the common electron-phonon interaction associated with the valence band39,40, in which a photo-excited carrier or above-gap optical transition is absent.

a RIXS spectra measured at the O-K edge, with σ (blue) and π (red) polarized light at T = 35K. The incident photon energies were selected according to the main peaks displayed by the O-K XAS, shown in (b). c Low-energy zoom-in of the RIXS spectra, measured for σ polarization (blue dots) at various incident photon energies. The spectra were fitted with five Voigt-shaped functions respectively centered at − 7 meV (v0), 0 meV (v1), 7 meV (v2), 14 meV (v3), and 36 meV (v4). The first four peaks are resolution-limited. The fit sum is represented by the blue solid line. Error bars indicate one standard deviation. Similar results are obtained for π polarization, see Supplementary Fig. 12. RIXS spectra showing full range of energy loss were also shown in Supplementary Fig. 12.
In summary, we present experimental evidence for the dominant coupling of the above-gap electronic transition to a phonon mode at 3.1 THz in the 2D ferroelectric semiconductor NbOI2. This mode is identified as the TO phonon mode, uniquely linked to the ferroelectric polarization, by Raman spectroscopy, pump-probe coherent spectroscopy, THz-TDS, and first principles calculation. Our findings provide direct evidence for the importance of specific forms of electron-TO phonon coupling in a 2D ferroelectric semiconductor. This is distinct from the well-known electron coupling to LO phonons in conventional semiconductors described by the Fröhlich model. The observed coupling to the TO phonon is specific to electronic excitation above the semiconductor bandgap and is absent for the valence band probed by RIXS spectroscopy.
Our finding reveals the distinct coupling of the above-gap electronic transition and associated photo-carriers to ferroelectric polarization through the soft TO phonon mode. While this type of coupling has been proposed for a range of paraelectric materials5,6,7,8,9, invoked in the ferroelectric polaron model for LHPs10,11,12,13 and Bi2O2Se14, and suggested for the ferroelectric semiconductor SbSI17, the unambiguous results presented here experimentally confirm the proposed charge carrier-TO phonon coupling. We believe this type of carrier-TO phonon coupling is of general importance for the efficient screening of the Coulomb potential and, thus, serving as a guiding principle in the search of defect tolerant semiconductors for optoelectronics from displacive ferro- or para-electric materials. Further, this coupling suggests a promising platform for realizing ultrafast modulation of polarization amplitude under sub-picosecond through optical excitation. Distinct from polarization switching enabled by strong THz field41, a pulse with visible-light frequency can launch ferroelectric TO phonon via the coupling we found. We suggest that this finding not only is of importance to understanding the electronic properties of 2D ferroelectric semiconductors but also shed light on the future development of ferroelectric devices with tunable polarization fields.